

#Empirical cdf pdf#
What do you think the unknown distribution looks like? Draw a rough sketch of a possible PDF for the unknown distribution.Cumulative Distribution Function Synopsis #include namespace boost std :: normal_distribution dis ( 0, 1 ) size_t n = 128 std :: vector v ( n ) for ( size_t i = 0 i / 8 4.52 ns ECDFConstructorSorted / 16 5.20 ns ECDFConstructorSorted / 32 5.22 ns ECDFConstructorSorted / 64 7.37 ns ECDFConstructorSorted / 128 7.16 ns ECDFConstructorSorted / 256 8.97 ns ECDFConstructorSorted / 512 8.44 ns ECDFConstructorSorted / 1024 9.07 ns ECDFConstructorSorted / 2048 11.4 ns ECDFConstructorSorted / 4096 12.6 ns ECDFConstructorSorted / 8192 11.4 ns ECDFConstructorSorted / 16384 16.0 ns ECDFConstructorSorted / 32768 17.0 ns ECDFConstructorSorted / 65536 19.5 ns ECDFConstructorSorted / 131072 15.8 ns ECDFConstructorSorted / 262144 17.9 ns ECDFConstructorSorted / 524288 26.7 ns ECDFConstructorSorted / 1048576 29.5 ns ECDFConstructorSorted / 2097152 31.8 ns ECDFConstructorSorted / 4194304 32.8 ns ECDFConstructorSorted / 8388608 35.4 ns ECDFConstructorSorted / 16777216 30.4 ns ECDFConstructorSorted _BigO 1.27 lgN ECDFConstructorSorted _RMS 20 % ECDFConstructorUnsorted / 8 155 ns ECDFConstructorUnsorted / 64 2095 ns ECDFConstructorUnsorted / 512 22212 ns ECDFConstructorUnsorted / 4096 220821 ns ECDFConstructorUnsorted / 32768 1996380 ns ECDFConstructorUnsorted / 262144 18916039 ns ECDFConstructorUnsorted / 2097152 194250013 ns ECDFConstructorUnsorted / 16777216 2281469424 ns ECDFConstructorUnsorted _BigO 5.65 NlgN ECDFConstructorUnsorted _RMS 6 % Shuffle / 8 82.4 ns Shuffle / 64 731 ns Shuffle / 512 5876 ns Shuffle / 4096 46864 ns Shuffle / 32768 385265 ns Shuffle / 262144 4663866 ns Shuffle / 2097152 54686332 ns Shuffle / 16777216 875309099 ns Shuffle _BigO 2.16 NlgN Shuffle _RMS 12 % ECDFEvaluation / 8 48.6 ns ECDFEvaluation / 64 61.3 ns ECDFEvaluation / 512 85.1 ns ECDFEvaluation / 4096 105 ns ECDFEvaluation / 32768 131 ns ECDFEvaluation / 262144 196 ns ECDFEvaluation / 2097152 391 ns ECDFEvaluation / 16777216 715 ns ECDFEvaluation _BigO 18.19 lgN ECDFEvaluation _RMS 60 % Generate some samples from the unknown distribution.How do the data points compare to the normal CDF? Is it clearer with a linear or probability scale? Generate some samples from one of the skewed distributions.
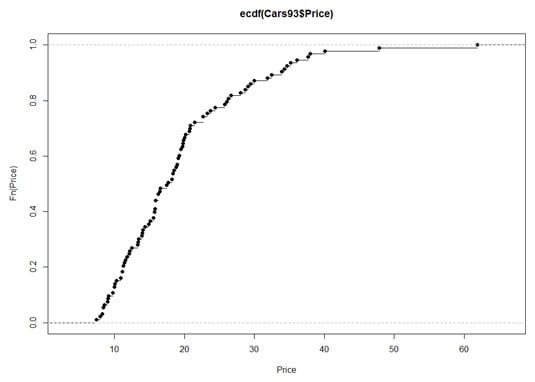
How do the data points compare to the normal CDF? Generate some samples from a normal distribution.Drag the dashed green line up and down to see how the two vertical axes are related. .Empirical CDF and Related Graphs 5.5.1 The Concept of the Empirical cdf (ecdf) 5.5.2 Probability Plots 5.5.3 Empirical Example: Exchange Rate Data. Click 'Show normal curve' to see the normal distribution that the probability scale is based on. Click 'Probability scale' to transform the vertical axis to a probability scale. Click 'Show normal CDF' to show the CDF of a normal distribution with the same mean and standard deviation as the sample.Īt first, the vertical axis shows the quantiles on a linear scale. Click 'New sample' to generate new data, or choose between a normal, left skewed, or right skewed distribution for sampling, or an unknown distribution.Ĭlick 'Show estimated CDF' to show an estimate of the empirical CDF based on the data. The applet initially shows data from a sample of size 19, sorted and plotted against the corresponding quantile on the vertical axis.


 0 kommentar(er)
0 kommentar(er)
